FIT CTU
Adam Vesecký
vesecky.adam@gmail.com
Lecture 7
Space
Architecture of Computer Games
Randomness
Randomness in games
Randomness is one of the most critical factors in ensuring an engaging game. Random events turn the game into a strict uncertainty, causing players to analyze the opportunity costs of their choices.
Random Generators
LCRNG
- Linear Congruential Random Number Generator
- starts with a seed value and performs some arithmetic operations which is both returned and used to reset the generator
- works best with prime values
- chosen well, they won't cycle until they nearly exhaust their domain
- used in rand() from standard C library
Lagged Fibonacci methods
- we are looking further back into the sequence of values
Carry methods
- takes part of the result from the previous stage and carries it forward to the least significant bits in the next stage
Random Generators
Mersenne Twister
- colossal period of 2^19937-1
- passes Diehard test
- uses SIMD vector instructions
Mother of all
- multiply-with-carry technique
- faster than twister, period of 2^250
Xoroshiro128+
- improved MOA, faster but less random
- used in many browsers for Math.random()
PCG Family
- simple fast space-efficient algorithms
- excellent statistical quality, very fast and compact

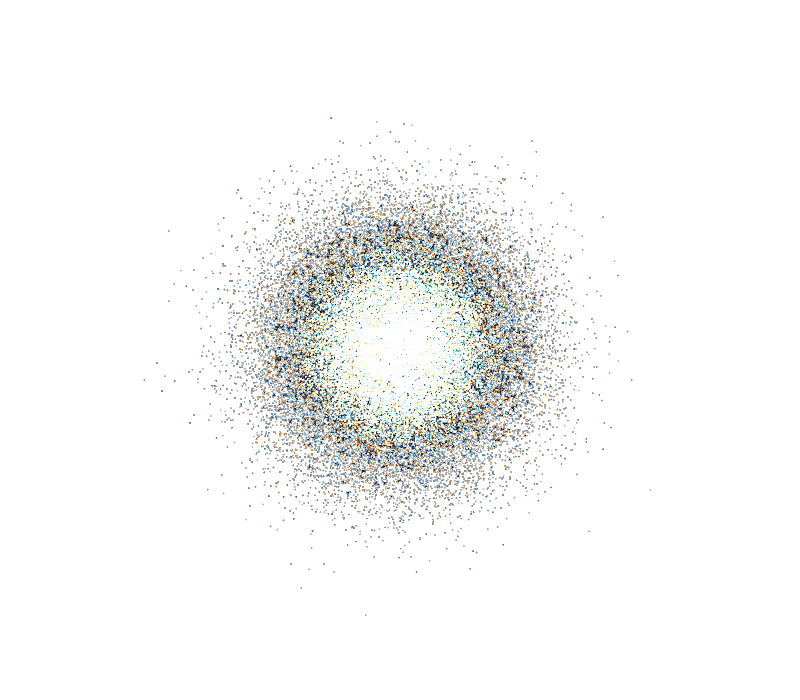
Random Functions Distribution


Doom
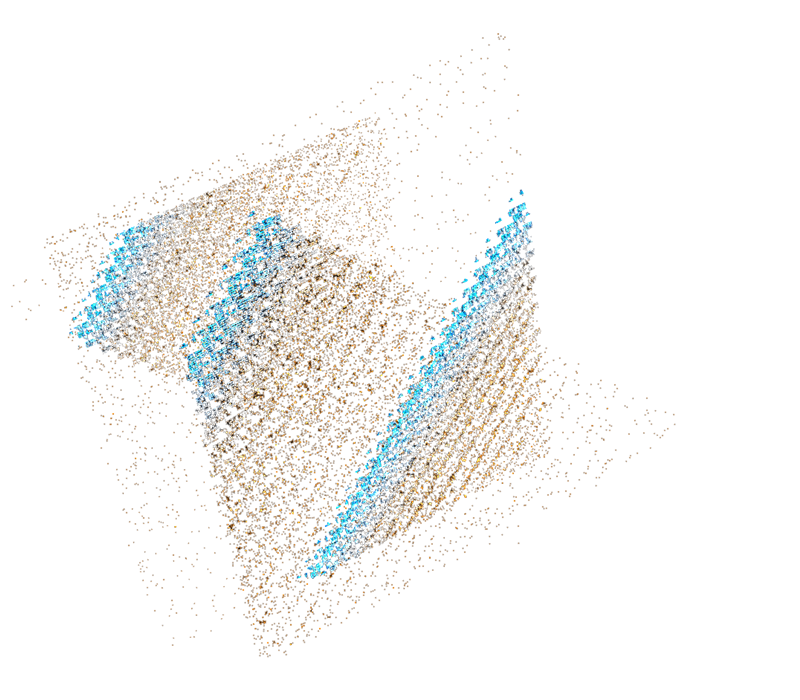

Transport Tycoon

Lehmer RNG

Gaussian MOA


Xorshift
Random Functions Distribution
Uniform distribution
- most common distribution of random generators
- applications: noise, shuffling, dice
Gaussian (normal) distribution
- more common in games - every characteristic has some kind of average, with individuals varying with a normal distribution
- can be calculated from a uniform generator via transformation (Box-muller algorithm)
- applications: height of trees, aiming for projectiles, average speed, physical reaction time, reload rate, refresh healing rate, critical hit
Uniform distribution
Gaussian distribution
Terms
Seed
- a hash that initializes random generators
- a good source of entropy is user input or time
Loot
- items obtained over the gameplay (money, spells, equipment, weapons,...)
Spinning
- calling the random function on a time-frame basis without using the result
- advances the game to a difficult-to-predict place
Rarity Slotting
- a method of standardization to determine rates (common, rare, epic, legendary)
- can be defined as a rarity table, calculated via weighted sum
Random encounter
- popular mechanics of RPG games (Final Fantasy, Pokémon, Golden Sun)
- the game suddenly shifts to battle mode, forcing the player to fight
- after winning the battle, the player receives a reward (skill upgrade, items, money)
Example: Random loot table
Randomness in games
Final Fantasy 1 (1987)
- reading sequentially from a list of pre-generated numbers (256 values in ROM)
- we could encounter the same group of enemies -> surprise determination
Super Mario 64 (1996)
- used LCRNG with 65114 possible states
- no spinning, the algorithm cycles only during certain events
Pokémon series for GBA (2002)
- in Ruby/Diamon/Emerald, the RNG is spun every frame
- Emerald sets the seed to zero on power-up
Darkwing Duck
- delaying a frame causes a different drop

Randomness in games
Pitfall! (1982)
- used linear-feedback shift register
- every screen is defined by 1 byte - 256 screens in total
- e.g. if a certain bit is 1, there is a water in the level

Doom (1993)
- the worst pseudo-random number generator ever
- a list of 256 random numbers cycled through
XCOM: Enemy Unknown (2012)
- no random spinning - dangerous when saving the game before taking an important shot
No Man's Sky (2016+)
- very little data is stored on the game's servers as all elements of the game are created through deterministic algorithms from a 64-bit seed
Example: Random Number Table in Doom
| 1 | unsigned char rndtable[256] = { |
| 2 | 0, 8, 109, 220, 222, 241, 149, 107, 75, 248, 254, 140, 16, 66 , |
| 3 | 74, 21, 211, 47, 80, 242, 154, 27, 205, 128, 161, 89, 77, 36 , |
| 4 | 95, 110, 85, 48, 212, 140, 211, 249, 22, 79, 200, 50, 28, 188 , |
| 5 | 52, 140, 202, 120, 68, 145, 62, 70, 184, 190, 91, 197, 152, 224 , |
| 6 | 149, 104, 25, 178, 252, 182, 202, 182, 141, 197, 4, 81, 181, 242 , |
| 7 | 145, 42, 39, 227, 156, 198, 225, 193, 219, 93, 122, 175, 249, 0 , |
| 8 | 175, 143, 70, 239, 46, 246, 163, 53, 163, 109, 168, 135, 2, 235 , |
| 9 | 25, 92, 20, 145, 138, 77, 69, 166, 78, 176, 173, 212, 166, 113 , |
| 10 | 94, 161, 41, 50, 239, 49, 111, 164, 70, 60, 2, 37, 171, 75 , |
| 11 | 136, 156, 11, 56, 42, 146, 138, 229, 73, 146, 77, 61, 98, 196 , |
| 12 | 135, 106, 63, 197, 195, 86, 96, 203, 113, 101, 170, 247, 181, 113 , |
| 13 | 80, 250, 108, 7, 255, 237, 129, 226, 79, 107, 112, 166, 103, 241 , |
| 14 | 24, 223, 239, 120, 198, 58, 60, 82, 128, 3, 184, 66, 143, 224 , |
| 15 | 145, 224, 81, 206, 163, 45, 63, 90, 168, 114, 59, 33, 159, 95 , |
| 16 | 28, 139, 123, 98, 125, 196, 15, 70, 194, 253, 54, 14, 109, 226 , |
| 17 | 71, 17, 161, 93, 186, 87, 244, 138, 20, 52, 123, 251, 26, 36 , |
| 18 | 17, 46, 52, 231, 232, 76, 31, 221, 84, 37, 216, 165, 212, 106 , |
| 19 | 197, 242, 98, 43, 39, 175, 254, 145, 190, 84, 118, 222, 187, 136 , |
| 20 | 120, 163, 236, 249 |
| 21 | }; |
| 22 | |
| 23 | int P_Random (void) { |
| 24 | prndindex = (prndindex+1)&0xff; |
| 25 | return rndtable[prndindex]; |
| 26 | } |

Procedural generation
Procedural content generation
- a content that is generated by algoritms
- the most common usecase - procedural textures
- unlimited number of possible structures
- lower storage overhead
- higher gameplay variety and replayability
- worse quality control
- we can generate an unplayable world
Games with procedural content
- Rogue (1980) - dungeons
- Diablo (1996) - dungeons
- OpenTTD (2004) - terrain
- Dwarf Fortress (2006) - game content, history, creatures
- Spore (2008) - creatures, civilizations, planets
- No Man's Sky (2016) - galaxies, planets, flora, fauna


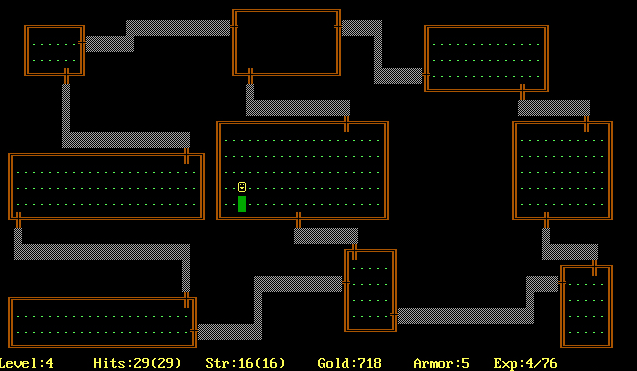
Procedural generators
Terrain generators
- noise generators
- box linear filters (box blur)
- midpoint displacement
Level generators
- cyclic generators
- marching squares
- rule-based generators
Pattern generators
- noise generators
- L-Systems
- markov chains
Filling space
- random walks
- cellular automata
- Poisson-disc sampling
- settling
- wang tiles
Partitioning space
- binary space partition
- voronoi diagrams
- dijkstra maps
- tree mapping
Example: Terrain generator
- generate a heightmap
- upscale the heightmap to desired resolution
- interpolate missing points
- apply effects (erosion, blur,...)


Example: 2D Level generator
- create a bounding box
- split the box into regions (axis-aligned binary splits)
- optional: skim perimeter regions
- place connections
- assign region types
- make adjustments
Example: Settling
- generate overlapping bounding boxes
- apply a repulsive force until they no longer overlap
- generate shapes
- generate paths
Noise
- Randomness is used to vary characteristics, noise is used to vary them over time or in space
- Noise functions
- Lattice-based
- Perlin noise, Simplex noise, Wavelet noise, Value noise
- Point-based
- Worley noise (Voronoi/Cellular)
- Lattice-based

Perlin Noise

Simplex Noise

Worley Noise
Perlin Noise
- Perlin Noise - developed by Ken Perlin in 1983
- Simplex Noise - Perlin's another noise, fewer artifacts and lower computational overhead
- both noises set a pseudo-random lattice in space and interpolate between respective points
- the noise is constructed from octaves (contribution to the signal at a particular scale)
- the signal is interpolated via a quartic function
| 1 | float PerlinNoise2D(int x, int y, float persistence, int octaves, float zoom) { |
| 2 | float total = 0.0f; |
| 3 | // initial frequency and amplitude |
| 4 | float frequency = zoom; |
| 5 | float amplitude = 1.0f; |
| 6 | |
| 7 | for (int i = 0; i < octaves; i++) { |
| 8 | // calculate noise |
| 9 | total = total + InterpolatedNoise(x*frequency, y*frequency) * amplitude; |
| 10 | // update frequency and amplitude |
| 11 | frequency = frequency * 2; |
| 12 | amplitude = amplitude * persistence; |
| 13 | } |
| 14 | return total; |
| 15 | } |
Fractals
- discovered in 1975
- geometric shapes that can be subdivided in parts, each of which is a reduced-size copy of the whole
- used for creating procedural textures and visual effects
- possible use in vast real-time game worlds is still a subject of discovery


Geometry
Homogeneous coordinates
- in Euclidean geometry we use Cartesian coordinates
- in projective geometry we use Homogeneous coordinates
- we can express all affine transforms and projections as one matrix
- transformations can be composed by matrix multiplication
- for points, for vectors
- Example: homogeneous matrix of a rotation matrix and a position vector
- Homogeneous coordinates -> Cartesian coordinates
- Cartesian coordiantes -> Homogeneous coordinates
Points and Vectors
- Cartesian coordinate system - by far the most common
- other systems: cylindrical, spherical
- in 2D engines, Y-axis is usually inverted
2D coordinate system
3D coordinate system
Points and Vectors
- Vector - a quantity that has both a magnitude and a direction
- vector can be used to represent a point, provided that we fix the tail of the vector to the origin of the coordinate system
Addition and subtraction
- vector + vector = vector
- vector - vector = vector
- point + vector = point
- point - point = vector
- point + point = undefined
Vector addition and subtraction
Points and Vectors
Magnitude
- scalar representing the length of the vector
Magnitude of a vector
Normalization
- a unit vector is a vector with a magnitude of one:
Normal vector
- vector is normal to a surface if it is perpendicular to it
Dot product
Dot Product
Cross product
- yields another vector that is perpendicular to two vectors
Example: Direction
- we want to rotate the bottom ship toward the other one
- we know
- calculate
- it is already normalized
- calculate
- normalize
- alternative:
Lines
- we have two points: and will take one step in direction for the second one:
- subtracting both, we get a vector with the same orientation
- all scalar multiplies of this vector from will generate points along the line
Example: closest point to a line
- given , we need to find closest to
- we compute the difference vector , then we project this onto to get
Rotation in 3D space
Rotational representations
Euler angles
- Pitch, Yaw, Roll
- simple, small size (3 floats), intuitive
- the order in which the rotations are performed matters
- gimbal lock issue - when a 90-degree rotation causes one axis to collapse onto another
Axis + angle
- axis of rotation plus a scalar for the angle of rotation
- intuitive and compact
- rotations cannot be easily interpolated
- rotations cannot be applied to vectors directly

Rotational representations
Quaternions
- similar to axis + angle, but with an algebraic twist
- alternative form:
- unit-length:
- a unit quaternion can be visualised as a 3D vector + scalar
- permits rotations to be concatenated and applied directly
- permits rotations to be easily interpolated
- can perform only one full rotation between keyframes
Rotation in affine space
Rotation about a fixed point
- move to the origin, rotate, move back
- post-multiply order -> right to left in the expresion and bottom to top in the code
- the origin of the object matters
OpenGL example:
| 1 | glPushMatrix(); |
| 2 | glTranslatef(250,250,0.0); // 3. Translate to the object's position. |
| 3 | glRotatef(angle,0.0,0.0,1.0); // 2. Rotate the object. |
| 4 | glTranslatef(-250,-250,0.0); // 1. Translate to the origin. |
| 5 | glPopMatrix(); |
Geometric hashing
World size
- diameter of the known universe:
- the smallest theoretical structure:
- 256 bits gives us values
- IEEE 754 format stores 24b of resolution in the mantissa: range of
- single precision, 32bit:
- double precision, 64bit:
- most games set their basic units as meter, making millimeter the smallest unit
- range areas for 32b numbers:
| Unit Size | Smallest Unit | Upper Range [m] | Upper Range Area |
|---|---|---|---|
| 100m | Space Ship | 1.67 x 10^9 | Diameter of the Sun |
| 1m | Car | 1.67 x 10^7 | Asia |
| 1cm | Coin | 1.67 x 10^6 | Mexico |
| 1mm | Fluid Particle | 1.67 x 10^5 | Paris |
| 100μm | Dust | 1.67 x 10^4 | Manhattan |
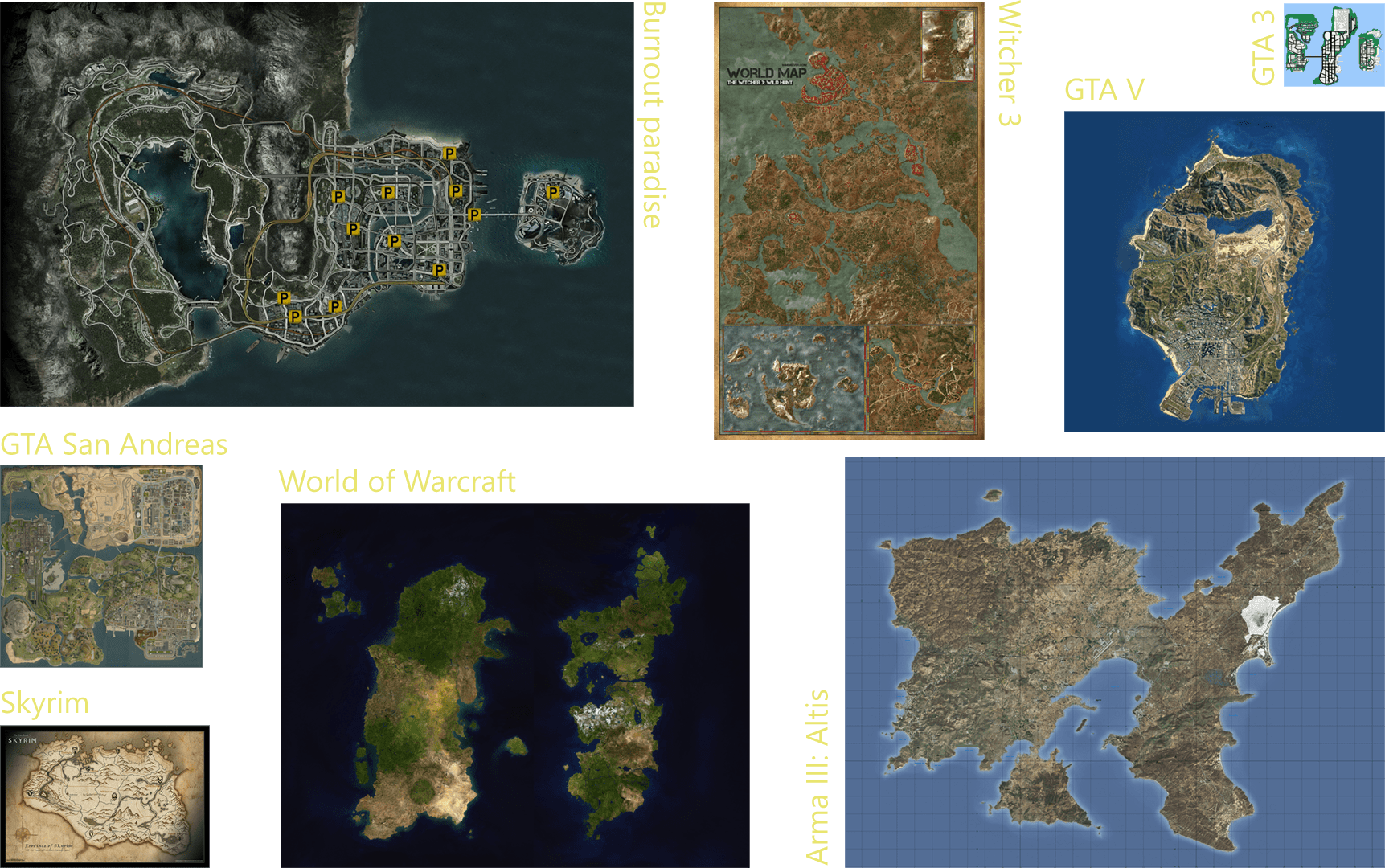
Map size comparison
IEEE 754 precision
- a quarter of all 32b numbers are in the range of , half of them in
- from 8 388 608 to 16 777 216, the precision for 32b is 1
- if the game world is too large, the precision close to borders may become insufficient
Spatial partitioning
Bounding volume
- groups objects or their parts together based on their positions and sizes
- if the object moves, so will the hierarchy
- used for physics, shape analysis, precise collision detection
Spatial data structure
- a structure that stores objects by their position
- is locked to the world
- used for range queries, neighborhood searching, rough collision detection
- the more objects we have, the more benefits we get
Implementations
- BSP - binary-space partitioning
- Quad-tree - for 2D and semi-3D space
- Oct-tree - for 3D space
- Grid - a square grid
Oct-tree
Binary Space Partitioning
- algorithm that decomposes a polygon-soup into a tree that contains convex sets
- first used in Doom to solve difficult rendering of circles around pillars in level 2
- very good for rendering, ray-casting and collision detection in complex indoor environments
- works only in static environments and requires a complex preprocessing stage
Quad-tree
- hierarchical partition
- each inner node has 4 children
- overlapping solid objects are put into all children they touch
- only objects in the same leaf can be in collision
- useful for outdoor scenes
- good for object sparsely spread that do not move too fast
Quad-tree and geometric hashing
Quad-tree for bounding boxes
Oct-tree
- doesn't need an expensive preprocessing stage
- allows very complex level geometry and easy editing
- the tree may contain a whole scene or only one object
- used for LoD, collision detection, voxel graphics,...
- no subdivision - 1 node
- 1 subdivision - 9 nodes
- 2 full subdivisions - 73 nodes
- 3 full subdivision - 585 nodes
Grid
- implemented as an 1D/2D/3D array or a hash-table
- each cell has a list of units that are inside
- if a unit crosses the boundary of the cell, we need to move it to the other list
- good for a large amount of fast objects that are uniformly distributed
- very fast to locate an object - in sharp contrast with recursing down a quad-tree
- takes up more memory, granularity is static
Navigation
Navigation
- essential feature for many games
Types
- local navigation in the environment (collision avoidance, ORCA)
- global navigation in the environment (pathfinding)
- navigation in a custom graph (e.g. task-based planning)

Navigation graph
- abstraction of all locations in a game environment the agents may visit
- enables game agents to calculate paths that avoid water, prefer traveling on roads to forest etc.
- may carry additional attributes (functions, type of a crossing etc.)
- waypoint-based, mesh-based, grid-based
- Node - position of a key area within the environment
- Edge - connection between those points
Navigation graph
Waypoint-based
- level designer places waypoints that are later linked up
Mesh-based
- created from a polygonal representation of the environment's floor
- describes walkable areas
Example: Unity mesh editor
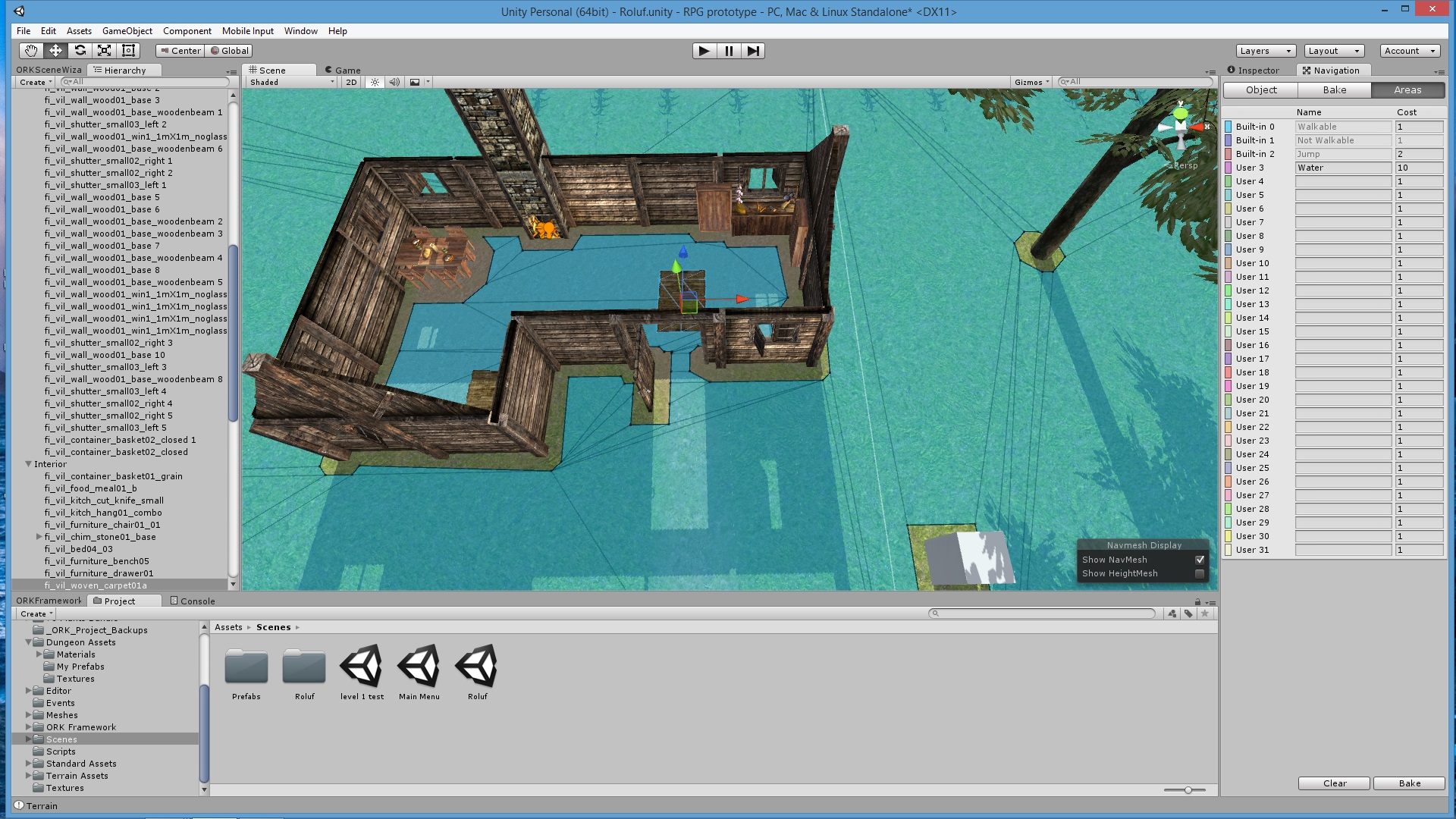
Example: Counter-strike mesh editor

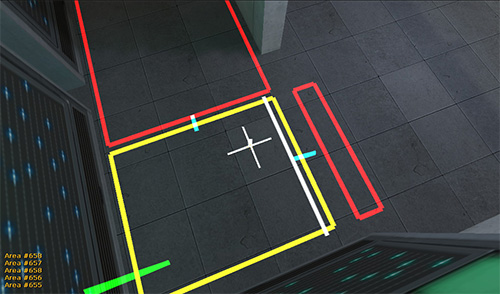

Navigation graph
Grid-based
- created by superimposing a grid over a game environment
- traversability flag indicates whether the cell is traversable or not
- connection geometries: tile, octile, hex
- reflecting renvironmental changes = recalculation of the traversability flag
Example: Connection geometry
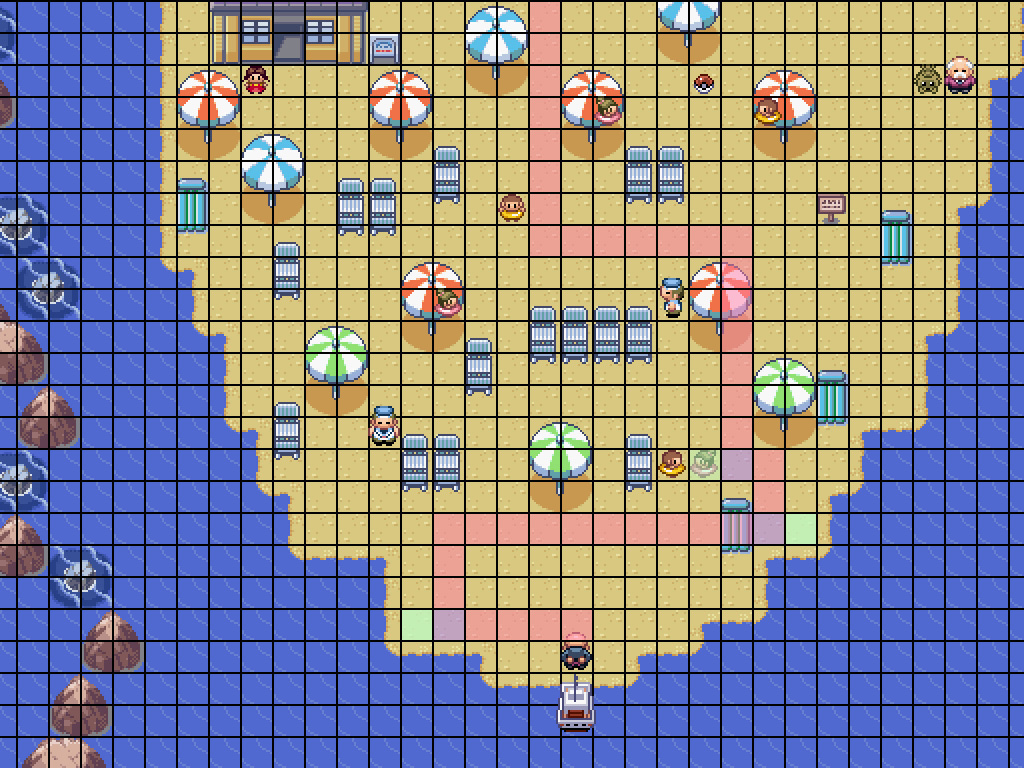
Pokémon series (Tile)

OpenTTD (Octile)
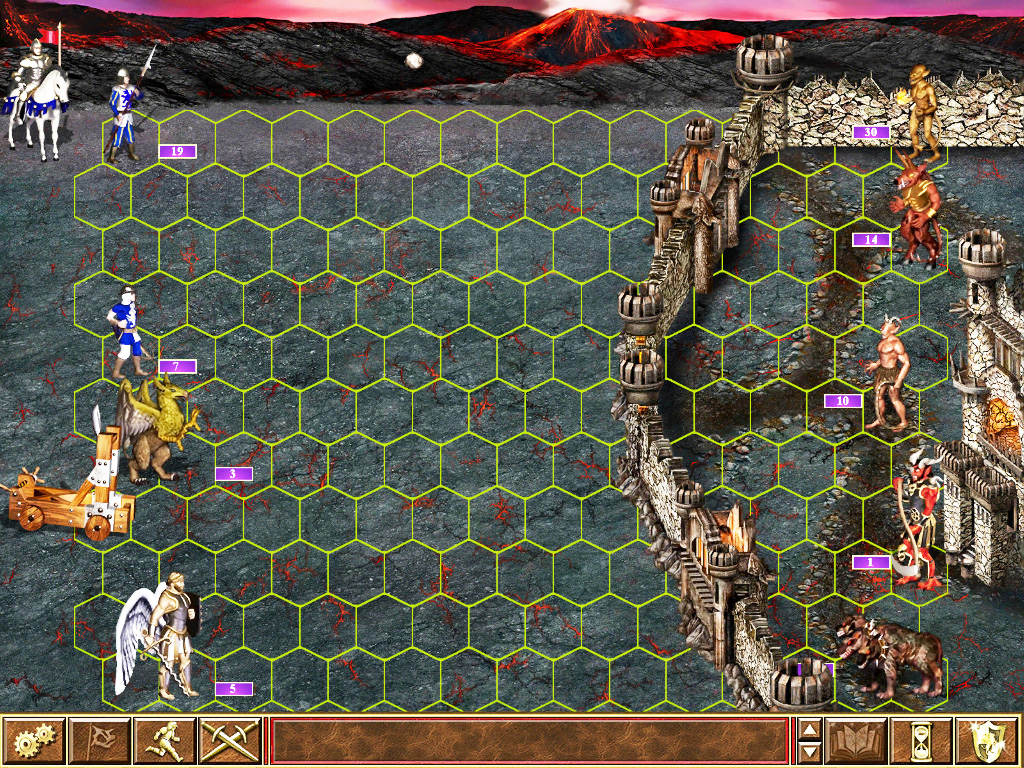
Heroes of M&M 3 (Hex)
Combined geometry
- units can move in any direction, static objects are located on a grid
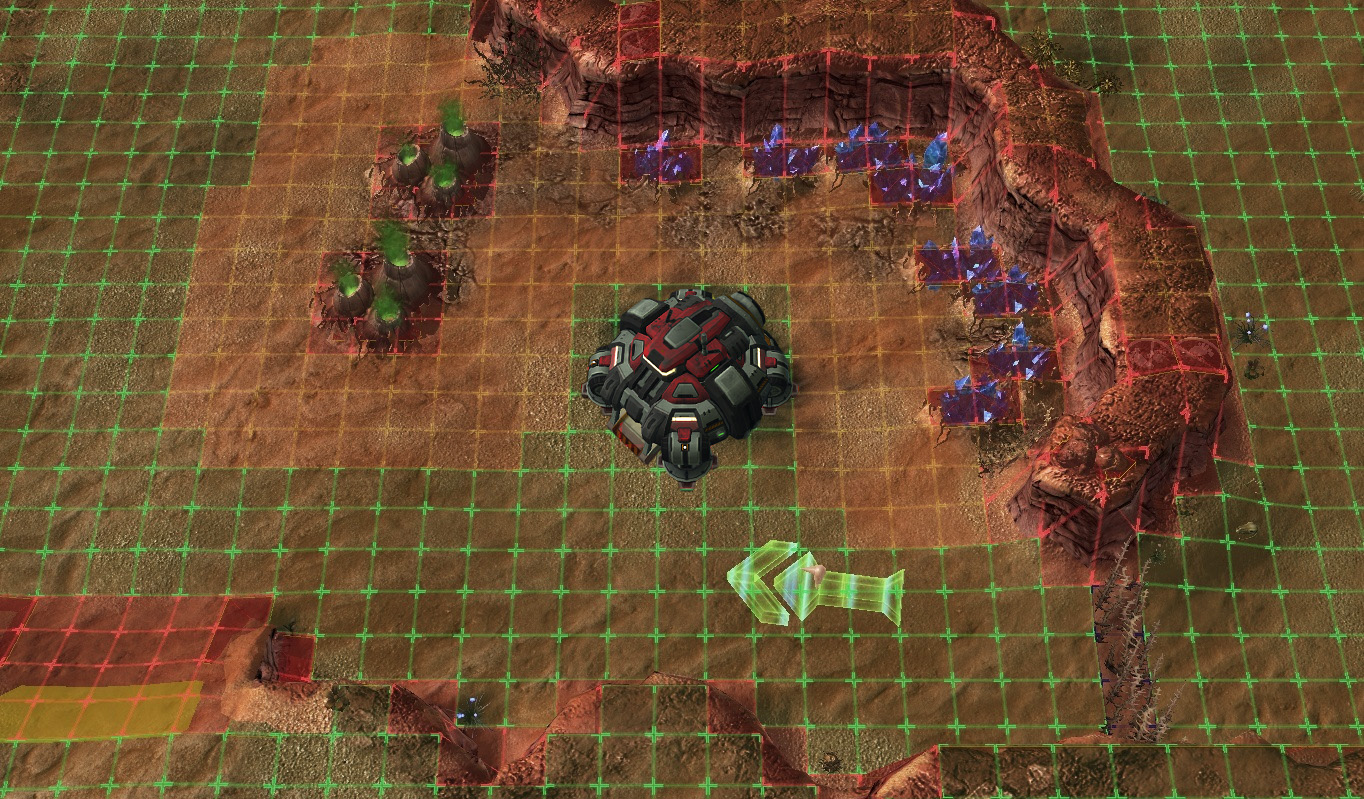
Starcraft II
Pathfinding
Properties
- completness - whether a solution is found or not
- optimality - quality of the solution found
- smoothing - whether the agent could move along the path smoothly
Environment type
- static - the map never changes during the gameplay
- dynamic - areas previously traversable can be obstructed later
- the higher the dynamicity, the higher the amount of replanning
NPC movement
- find the closest graph node to the NPC's current location: A
- find the closest graph node to the target location: B
- find path from A to B
- move to A
- move along the path to B
- move from B to target location

Pathfinding algorithms
Uniformed graph searches
- searches a graph without regard to any associated edge cost
- DFS (depth-first search)
- searches by moving as deep into the graph as possible
- doesn't guarantee to find the best path
- BFS (breadth-first-search)
- fans out from the source node, always finds the best path
Cost-based graph searches
- Dijkstra's Algorithm
- explores every node in the graph and finds the shortest path from the start node to every other node in the graph
- uses CSF (cost-so-far) metric
- explores many unnecessary nodes
- A* (Dijkstra with a Twist)
- extension of Dijkstra, invented in 1968
- main difference: augmentation of the CSF value with a heuristic value
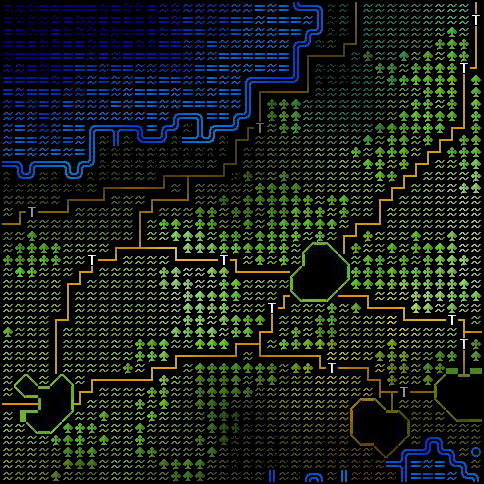
A*
- improved Dijkstra by an estimate of the cost to the target from each node
- Cost , where is the cost-so-far and is the heuristic estimate
- Heuristics: Euclidean, Manhattan, adaptive, dynamic,...
- Manhattan distance will work if almost no obstacles appear
Improvements
- preprocess the map, calculate universal paths
- mark tiles which cannot lead anywhere as dead-ends
- limit the search space
Pathfinding algorithms: Comparison
- breadth-first search ignores the cost
- Dijkstra ignores the topology of the graph
- A* considers both
HPA*: Hierarchical Pathfinding A*
- uses a fixed-size clustering abstraction (problem subdivision)
- divides the navgraphs into regions, transitions are connected by intra-edges
- gate - longest obstacle-free segment along a border
- fast enough for most games, but requires semi-static environment
- 3 stages: build an abstract graph, search the abstract graph for an abstract path, refine the abstract path into a low-level path
Lecture Summary

- I know what purpose can serve uniform and gaussian distributions
- I know what is a loot, spinning, rarity slotting and random encounter in games
- I know something about noise functions
- I know basic vector operations: addition, subtraction, magnitude, normalization, and dot product
- I know what quaternions and Euler angles are, and what use-cases they are good for
- I know basic structures for spatial partitioning: grid, quad-tree, oct-tree and BSP
- I know basic types of navigation graphs
- I know something about pathfinding algorithms, such as BFS, Dijkstra and A*
Goodbye Quote
Forgiveness is a concern of the living.Arthas, Warcraft 3

